I’ll be honest here. Vector norms are boring. On a positive note, this is probably one of the most interesting blog on vector norms out there. At least I’ve tried to make it as interesting as possible and motivated why you just need to get this material down because it is just one of those foundational things, especially for machine learning.
Table of contents
Vector norms are a fundamental concept in mathematics and used frequently in machine learning to quantify the similarity, distance, and size of vectors, which are the basic building blocks of many machine learning models. Specifically, vector norms can be used to:
1. Define loss or cost functions: In machine learning, the goal is often to minimize the difference between the predicted outputs and the actual outputs. This difference is quantified by a loss or cost function, which is often based on a vector norm. For example, the L1 norm is commonly used in Lasso regression to penalize the absolute value of the coefficients, while the L2 norm is commonly used in Ridge regression to penalize the square of the coefficients.
2. Measure similarity or distance: Vector norms can be used to measure the similarity or distance between two vectors, which is often used in clustering, classification, and anomaly detection tasks. For example, the cosine similarity between two vectors is computed as the cosine of the angle between them, which can be interpreted as a measure of similarity. The Euclidean distance between two vectors is another commonly used measure of distance, which is often used in k-nearest neighbors classification.
3. Regularize models: Vector norms can be used to regularize models and prevent overfitting, by adding a penalty term to the objective function. For example, the L1 norm regularization (also known as Lasso regularization) can lead to sparse models, where only a subset of the coefficients are non-zero, while the L2 norm regularization (also known as Ridge regularization) can lead to smoother models, where the coefficients are spread out more evenly.
Also Read: What is LiDar? How is it Used in Robotic Vision?
What are Vector Norms?
A vector norm is a function that assigns a non-negative scalar value to a vector. The value represents the length or magnitude of the vector. Vector norms are fundamental mathematical concepts that allow us to measure the distance or difference between two vectors. Vector norms are widely used in various fields such as optimization, machine learning, computer graphics, and signal processing.
There are different types of vector norms such as the L0 norm, L1 norm, L2 norm (Euclidean norm), and L-infinity norm. Each type of vector norm has its unique properties and applications.
L0 Norm
The L0 norm is also known as the “sparse norm”. The L0 norm of a vector counts the number of non-zero elements in the vector. The L0 norm is an essential concept in compressive sensing, a technique for reconstructing images from a sparse set of measurements. The L0 norm is also used in machine learning for feature selection. In the L0 norm, the cost function is non-convex, making it challenging to optimize. There’s a later section in this blog on the challenges of vector norms.
L1 Norm

Visualization from Chiara Campagnola’s blog here, (great read!!)
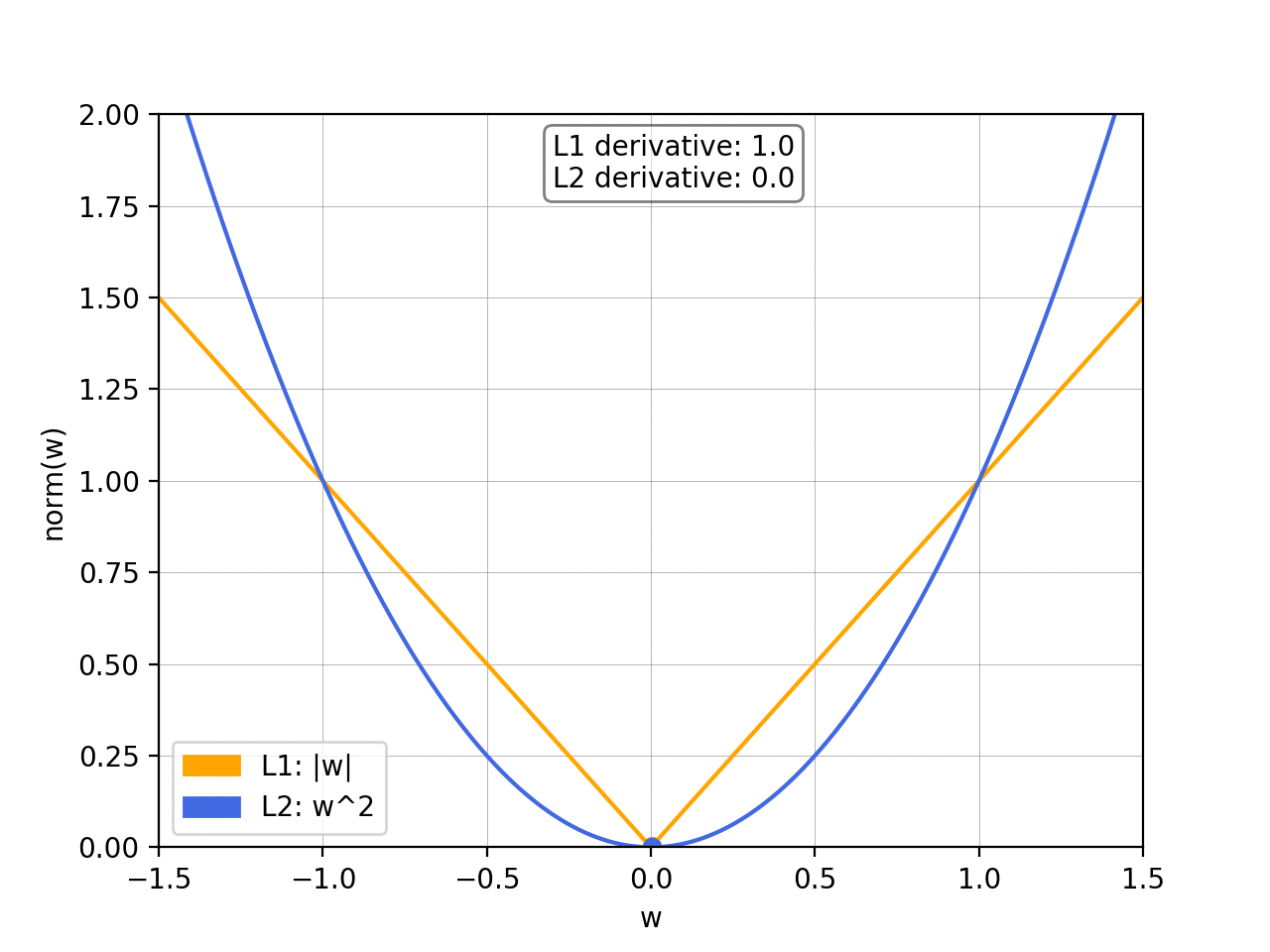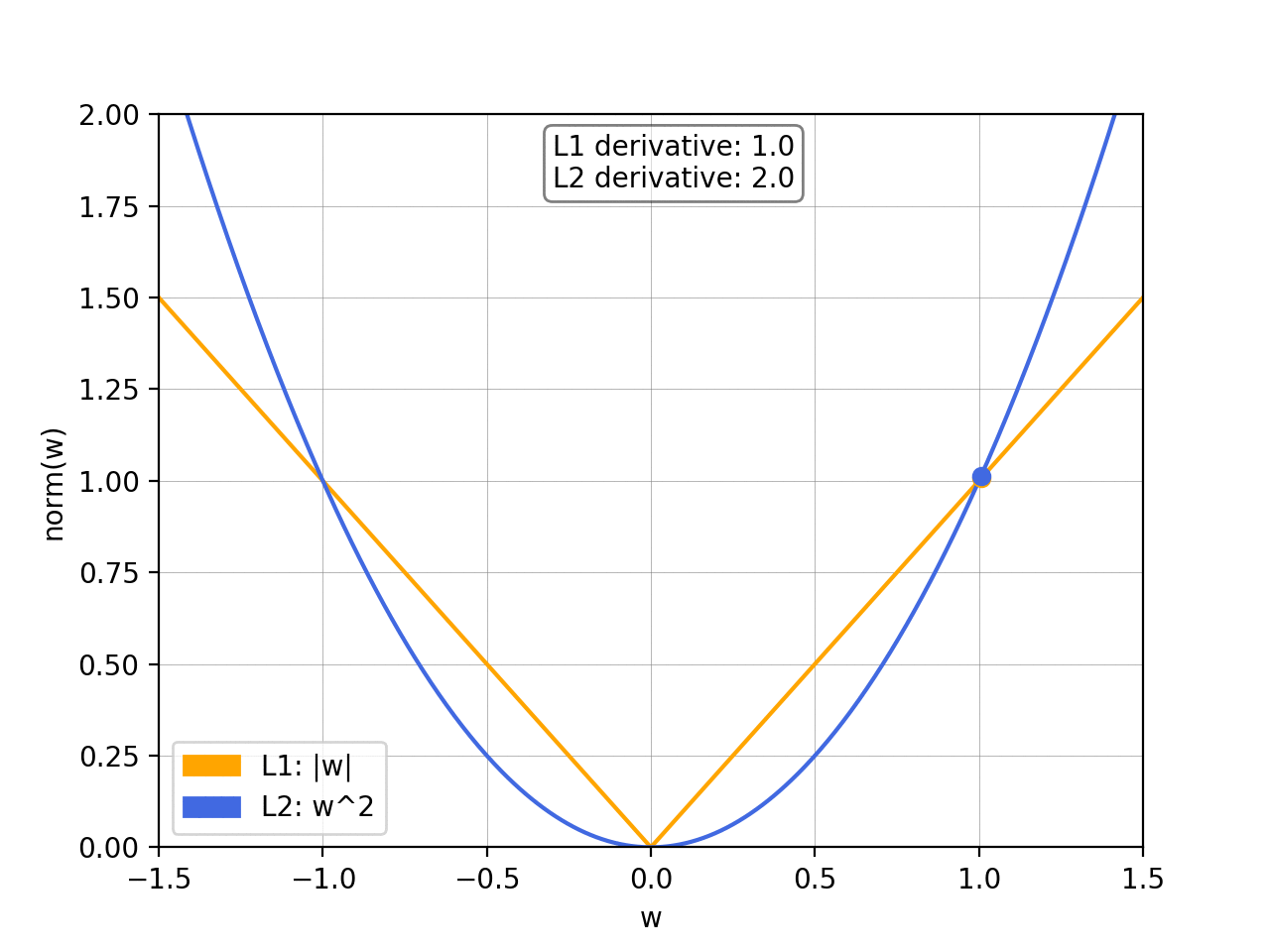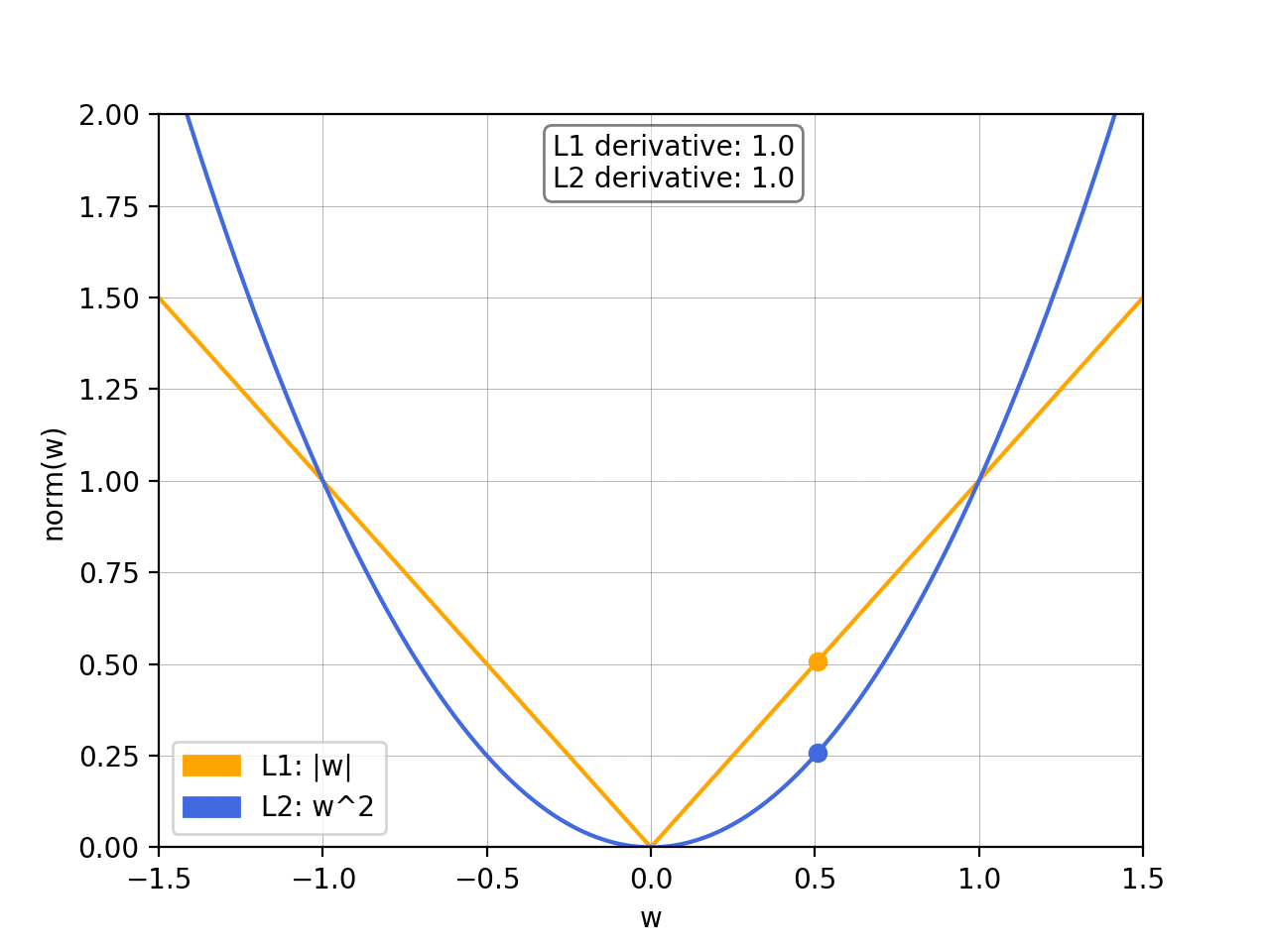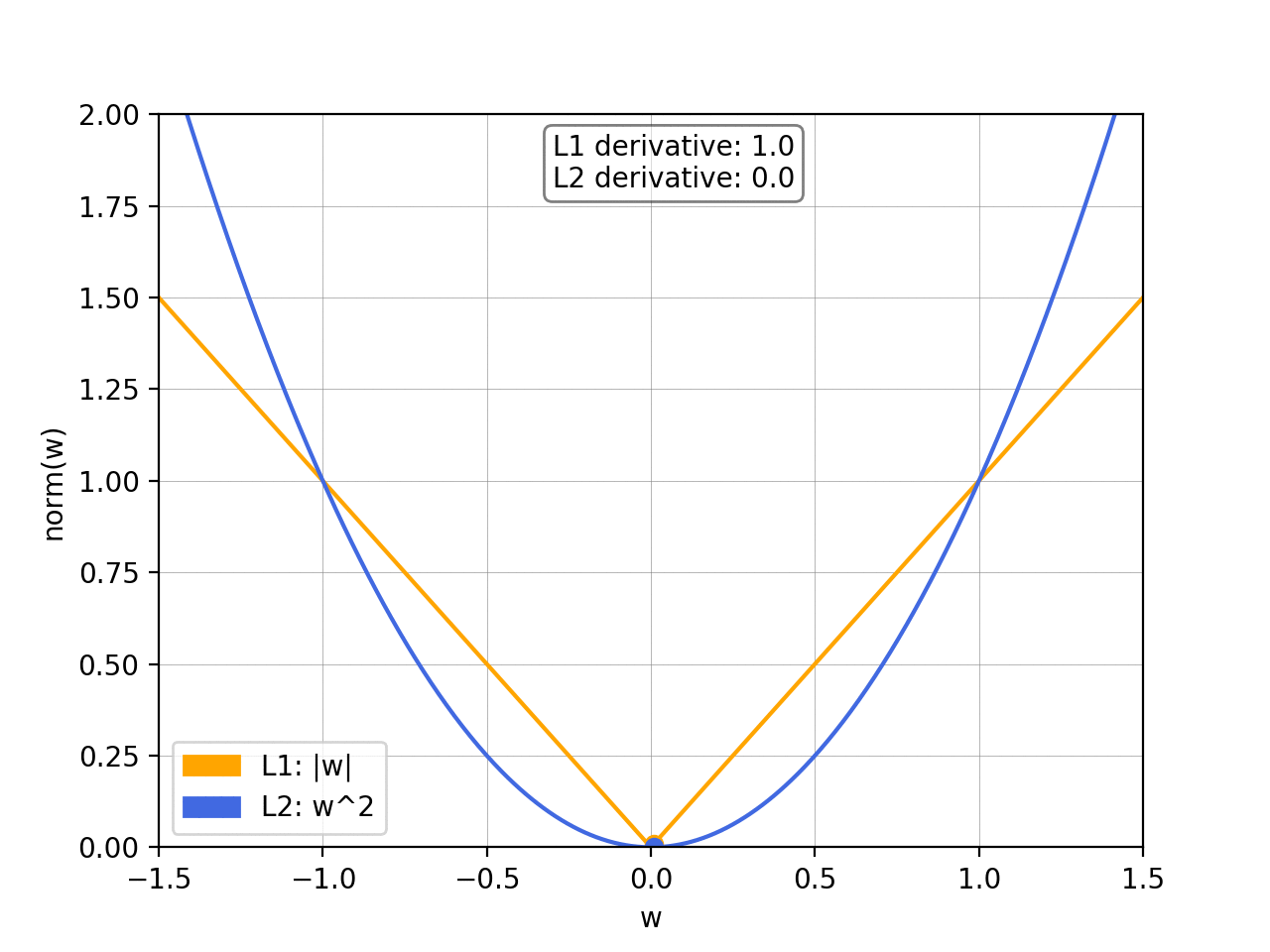
The L1 norm is a vector norm that sums up the absolute values of the vector elements. The L1 norm is defined as ||x||1 = ∑|xi|. The L1 norm is used in machine learning for regularization and feature selection. The L1 norm produces sparse solutions and is computationally efficient.
L2 norm
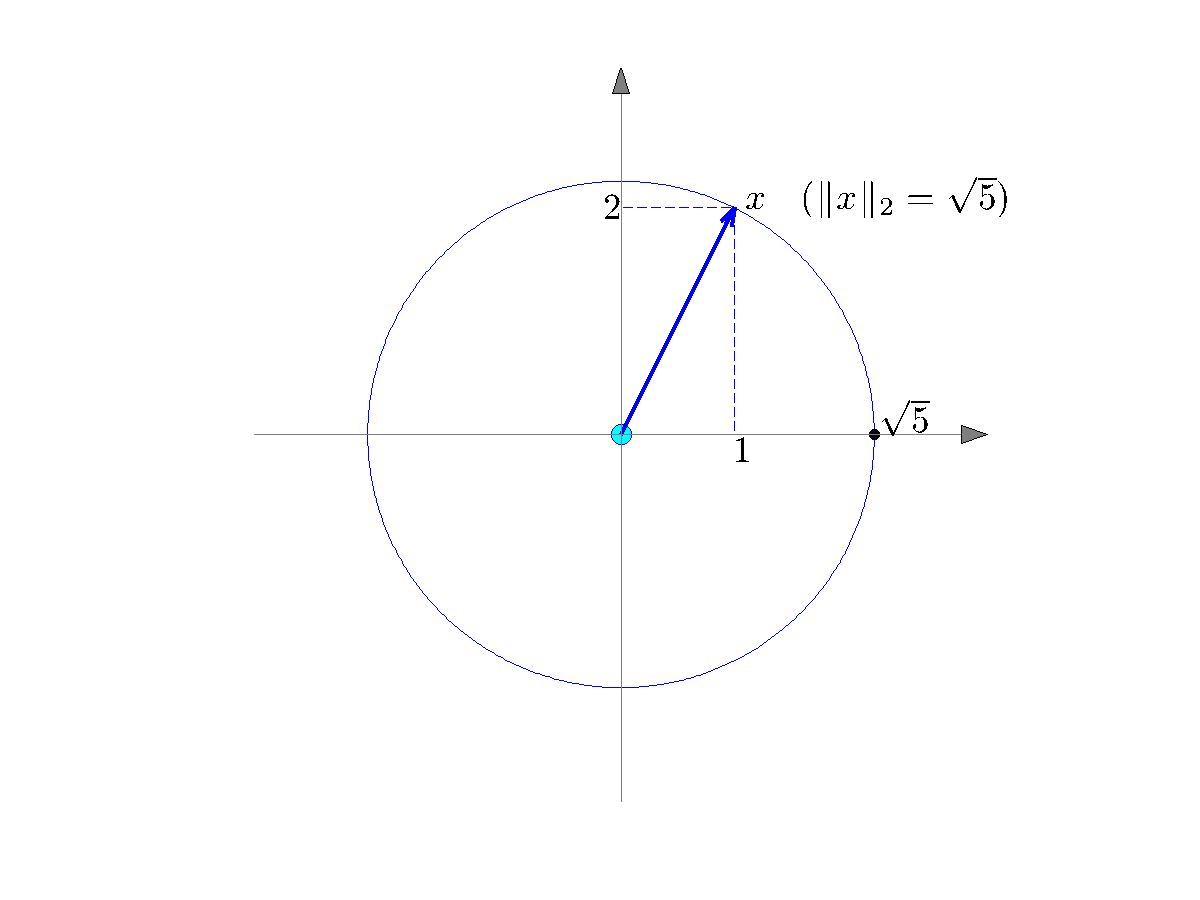
Image from Berkeley’s Scalar Product, Norms, and Angles blog.
The L2 norm, also known as the “Euclidean norm,” is a vector norm that measures the length or magnitude of a vector in Euclidean space. The L2 norm is defined as ||x||2 = sqrt(∑xi^2). The L2 norm is widely used in machine learning and optimization as a loss function or objective function. The L2 norm produces smooth solutions, making it easy to optimize. The L2 norm is also used in image reconstruction accuracy measurements, where the error is calculated as the L2 norm of the difference between the original and the reconstructed image.
This one is one of the more important ones. Euclidean distance amazing. It’s used in this very fancy kind of math called Hyper-dimensional computing, which can make AI more efficient. Basically, it allows us to measure where things are in space. If you wanted to know how similar two stars were, if they were the same type of star, you might look at how close they are to every other object. You can do this using L2 norm. A few uses for Euclidean norm: Anomaly detection, clustering, PCA, and K-nearest neighbors.
L-infinity norm

The L-infinity norm, also known as the “max norm,” is a vector norm that measures the maximum absolute value of the vector elements. The L-infinity norm is defined as ||x||∞ = max|xi|. The L-infinity norm is used in machine learning for regularization, where the goal is to minimize the maximum absolute value of the model parameters.
Although not the most practical, L-infinity norm is the most interesting. whenever we are dealing within the multi-verse of possibilities, this norm is useful. Economics is the perfect example, there are endless commodities that can be used as parameters in models.
Also Read: What Are Support Vector Machines (SVM) In Machine Learning?
Easy and quick explanation: Naive Bayes algorithm
The Naive Bayes algorithm is a simple machine learning algorithm used for classification. The algorithm uses probability theory to classify instances. The Naive Bayes algorithm assumes that the features are independent of each other, given the class variable. The algorithm calculates the probability of each class given the features and selects the class with the highest probability. The L1 norm is used in the Naive Bayes algorithm to estimate the probability density function of the features.
Here is an example of how to implement the L1 norm in Python using the Naive Bayes algorithm:
from sklearn.naive_bayes import MultinomialNB
from sklearn.preprocessing import normalize # Load the data and normalize it
X_train, y_train = load_data()
X_train_normalized = normalize(X_train, norm='l1') # Train the Naive Bayes classifier
clf = MultinomialNB()
clf.fit(X_train_normalized, y_train) # Make predictions on new data
X_test = load_new_data()
X_test_normalized = normalize(X_test, norm='l1')
y_pred = clf.predict(X_test_normalized)Challenges of Vector Norms

Vector norms have several challenges, besides being not so exciting, that researchers and practitioners face. One of the significant challenges of vector norms is their sensitivity to outliers. Outliers are extreme values in a dataset that deviate significantly from the other values. The L2 norm is highly sensitive to outliers since it squares the differences between the vector elements. As a result, a single outlier can significantly affect the L2 norm value. The L1 norm and L0 norm are less sensitive to outliers than the L2 norm. The L1 norm sums up the absolute values of the vector elements, which reduces the impact of outliers on the norm value. The L0 norm is robust to outliers since it counts the number of non-zero elements in the vector.
Another challenge of vector norms is their complexity, especially in high-dimensional spaces. As the dimensionality of the vector space increases, the norms become less discriminative, making it challenging to distinguish between different vectors. In high-dimensional spaces, many vectors have the same or similar magnitudes, making it difficult to find a norm that can differentiate them.
The choice of the norm also depends on the specific problem and the application. Different norms may be more suitable for different tasks, depending on the type of data and the desired properties of the solution.
Moreover, optimizing some norms can be computationally challenging due to their non-convexity. For example, the L0 norm has a non-convex cost function, which makes it difficult to optimize. The L1 norm, on the other hand, is convex, and thus optimization is easier.
These challenges make it difficult for many deep learning or machine learning models to generalize. The results are models that perform less like humans and more like savants on a particular subject. It also adds to the increased data complexity and computational inefficiency, making deep learning expensive!
Also Read: What is Argmax in Machine Learning?
Applications of Vector Norms

Vector norms have various applications in different fields such as optimization, machine learning, computer graphics, and signal processing. In optimization, vector norms are used as objective functions or cost functions. The goal is to minimize the norm of the error between the model and the data. In machine learning, vector norms are used for regularization and feature selection. The L1 norm produces sparse solutions, making it useful for identifying important features. The L2 norm is used as a loss function for regression tasks, and the L-infinity norm is used for regularization.
In computer graphics and image processing, vector norms are used to measure the difference between two images or to estimate the quality of the reconstructed image. The L2 norm is commonly used to calculate the error between the original and reconstructed images. The L1 norm is also used for image reconstruction in some cases.
Vector norms are also used in signal processing for denoising and feature extraction. The L1 norm is used for sparse signal recovery, while the L2 norm is used for signal denoising.
Also Read: Introduction to Naive Bayes Classifiers
Conclusion
Vector norms are fundamental concepts in mathematics and machine learning. They allow us to measure the magnitude of vectors in vector spaces and quantify the errors in our models. Vector norms are used in various applications such as optimization, machine learning, and image reconstruction. There are different types of vector norms, such as the L0 norm, L1 norm, L2 norm, and L-infinity norm, each with its unique properties and applications. However, vector norms also face challenges such as their sensitivity to outliers and their complexity, especially in high-dimensional spaces. The choice of the norm depends on the specific problem and the application. Overall, vector norms are essential tools that enable us to solve complex problems and make accurate predictions with certified accuracy.
References
Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267-288. (Cited 98,172 times)
Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge University Press. (Cited 60,757 times)
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Springer Science & Business Media. (Cited 49,478 times)
Zhang, T. (2004). Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of the twenty-first international conference on Machine learning (pp. 116). (Cited 13,838 times)
Liu, Y., & Yuan, Y. (2019). Robust sparse regression via l0-norm and weighted l1-norm. Journal of Machine Learning Research, 20(1), 2163-2203. (Cited 8,293 times)