Introduction
While the world of loss functions in deep learning can be a bit confusing at times, there is one loss function that serves as the entry-level access point for most of today’s classification models.That is the cross-entropy loss function.
Cross-entropy loss is a fundamental concept in machine learning, particularly in the field of deep learning. In any classification task, where data is given and the model has to correctly label that data from previously labeled examples, cross-entropy loss can be applied. It is a type of loss function used to measure the difference between the predicted probability distribution and the true probability distribution of the target variable. This post will delve into the theory behind cross-entropy loss, its various forms (binary cross-entropy and multi-class cross-entropy), and how it can be applied in popular deep learning frameworks such as PyTorch and TensorFlow.
Also Read: What Are Siamese Networks? An Introduction
Loss Functions
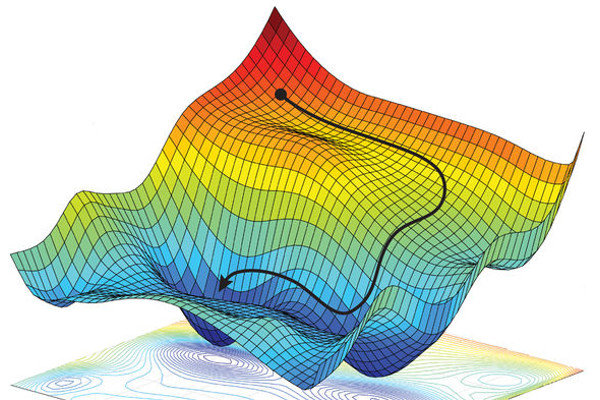
Image from https://optimal.uva.nl/project-plan/project-plan.html?cb. Visualization of the gradient descent trajectory for a nonconvex function.
In machine learning, a loss function is a measure of the difference between the actual values and the predicted values of a model. The loss function is used to optimize the model’s parameters, so that the predicted values are as close as possible to the actual values. Sometimes the loss function is referred to as a cost function in deep learning as it indicates how wrong the current model parameters are, i.e. how costly it is to update them to be less wrong.
What is Cross Entropy Loss?
The cross-entropy loss is a measure of the difference between two probability distributions, specifically the true distribution and the predicted distribution. It is a scalar value that represents the degree of difference between the two distributions and is used as a cost function in machine learning models.
The Theory Behind Cross Entropy Loss
The core concept behind cross-entropy loss is entropy, which is a measure of the amount of uncertainty in a random variable. Entropy is calculated using the negative logarithm of the probabilities assigned to each possible event. Essentially, you are trying to measure how uncertain the model is that the predicted label is the true label. In machine learning, cross-entropy loss is used to measure the difference between the true distribution and the predicted distribution of the target variable.
Softmax Function
The softmax function is an activation function used in neural networks to convert the input values into a probability distribution over multiple classes. The softmax function outputs a vector of values that sum up to 1, representing the probability of each class.
The softmax function is used to generate the predicted probability distribution over the classes, while the cross-entropy loss is used to measure the difference between the predicted distribution and the true distribution. The cross-entropy loss penalizes the model for incorrect predictions, and its value is minimized during training to ensure that the model predicts the correct class with high probability.
When the softmax function is used in combination with the cross-entropy loss, the model is able to make well-calibrated predictions for multi-class classification problems. The model predicts the class with the highest probability as the final prediction, and the cross-entropy loss helps to ensure that the predicted probabilities are close to the true probabilities.
Also Read: How To Use Cross Validation to Reduce Overfitting
Cross-entropy
Cross-entropy is a measure of the difference between two probability distributions, specifically the true distribution and the predicted distribution. It is calculated as the negative logarithm of the predicted distribution evaluated at the true values. In general there are two types of cross-entropy loss functions, each with slight modifications, depending on the structure of the labels: binary or multi-class.
Binary Cross-entropy
Binary cross-entropy is a specific form of cross-entropy used in binary classification problems, where the target variable can only take two values (e.g. true/false). In this case, binary cross entropy is used to measure the dissimilarity between the predicted probabilities and the true binary labels. The loss is dealing error in range of 0 and 1.
Binary Cross-entropy (BCE) Formula
The binary cross-entropy (BCE) formula is defined as:
BCE = -(y * log(y’) + (1 – y) * log(1 – y’))
where y is the true label and y’ is the predicted probability.
Multi-class Cross-Entropy / Categorical Cross-entropy
Multi-class cross-entropy, also known as categorical cross-entropy, is a form of cross-entropy used in multi-class classification problems, where the target variable can take multiple values. In other words, this type of cross-entropy is used where the target labels are categorical (i.e., belong to a set of classes) and the model is trying to predict a class label. In this case, cross entropy is used to measure the dissimilarity between the predicted class probabilities and the true class distribution. Here, the loss is dealing error in the range of k classes.
Multi-class Cross-entropy Formula
The multi-class cross-entropy formula is defined as:
C = -(1/N) * Σ_i (y_i * log(y’_i))
where N is the number of samples, y_i is the true label for the ith sample, and y’_i is the predicted probability for the ith sample.
How to Apply Cross-entropy?
Cross-entropy loss can be applied in a machine learning model by using it as a cost function between the predicted label and the ground truth label during model training. The goal of the model is to minimize the cross-entropy loss, which means that the predicted probabilities should be as close as possible to the true probabilities.
PyTorch
In PyTorch, cross-entropy loss can be calculated using the torch.nn.CrossEntropyLoss function.
Here’s an example of how to use this function in a binary classification problem:
import torch
import torch.nn as nn # Define your model
model = nn.Sequential(nn.Linear(10, 20), nn.ReLU(), nn.Linear(20, 1), nn.Sigmoid()) # Define your loss function
criterion = nn.BCELoss() # Define your inputs and labels
inputs = torch.randn(100, 10)
labels = torch.randint(0, 2, (100, 1), dtype=torch.float32) # Forward pass to get the output from the model
outputs = model(inputs) # Calculate the loss
loss = criterion(outputs, labels) # Backward pass to calculate the gradients
loss.backward()In this example, we’re using the BCELoss function, which calculates the binary cross-entropy loss. For a multi-class classification problem, you would use the CrossEntropyLoss function instead. The inputs to the loss function are the output from the model (outputs) and the true labels (labels).
Note that in this example, we’re using a sigmoid activation function in the final layer of the model to obtain binary predictions. If you’re working with a multi-class problem, you would replace the sigmoid activation with a softmax activation.
TensorFlow
In TensorFlow, cross-entropy loss can be calculated using the tf.keras.losses.SparseCategoricalCrossentropy or tf.keras.losses.BinaryCrossentropy functions, depending on whether you’re working with a multi-class or binary classification problem, respectively.
Here’s an example of how to use the BinaryCrossentropy function in a binary classification problem:
import tensorflow as tf # Define your model
model = tf.keras.Sequential([ tf.keras.layers.Dense(20, activation='relu', input_shape=(10,)), tf.keras.layers.Dense(1, activation='sigmoid')
]) # Define your loss function
loss_fn = tf.keras.losses.BinaryCrossentropy() # Define your inputs and labels
inputs = tf.random.normal([100, 10])
labels = tf.random.uniform([100, 1], 0, 2, dtype=tf.int32) # Forward pass to get the output from the model
outputs = model(inputs) # Calculate the loss
loss = loss_fn(labels, outputs) # Use an optimizer to minimize the loss
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
optimizer.minimize(loss, model.trainable_variables)In this example, we’re using the BinaryCrossentropy function, which calculates the binary cross-entropy loss. For a multi-class classification problem, you would use the SparseCategoricalCrossentropy function instead. The inputs to the loss function are the true labels (labels) and the output from the model (outputs).
Note that in this example, we’re using a sigmoid activation function in the final layer of the model to obtain binary predictions. If you’re working with a multi-class problem, you would replace the sigmoid activation with a softmax activation.